Question 1
Given that log₁₀5 = x and log₁₀11 = y, express log₁₀275 in terms of x and y.
Login to check if your answer is correct.
Question 2
The sets P = {x:x = 3, 5, 6} and Q = {x: 2 ≤ x ≤ 5} are subsets of μ = {x: 1 ≤ x ≤ 10, where x is an integer}. Find P' ∩ Q.
Login to check if your answer is correct.
Question 3
A pyramid has a rectangular base of length 6.5 cm and width 4.2 cm. If the height of the pyramid is 12 cm, find the volume.
Login to check if your answer is correct.
Question 4
Given that \((1 \tfrac{2}{3})^{\tfrac{x}{2}} = (4 \tfrac{17}{27})\), find the value of \(x\).
Login to check if your answer is correct.
Question 5
The first 4 terms of an Arithmetic Progression (A.P) are 8, x , y and 17. Find the value of \((x + y)\).
Login to check if your answer is correct.
Question 6
In a test, the mean mark of 25 students in a class, P, is 72.2 and the mean mark of 20 students in another class, Q, is 65. Find the mean mark of all the students in P and Q.
Login to check if your answer is correct.
Question 7
Mr. Gyan bought a car for USD 16,800.00 and later sold it at 85 % of the original cost. He spent USD 3,930.75 from the money he received from the sale of the car and invested the remaining at 18 % per annum simple interest. How much interest did he earn in 9 years?
Login to check if your answer is correct.
Question 8
The mean and range of 1.20, 1.00, 0.90, 1.40, 0.80, 0.80, 1.20 and 1.10 are m and r respectively. Find the value of \((m + r)\)
Login to check if your answer is correct.
Question 9
Given that \(\dfrac{3}{x+y} - \dfrac{4}{x-y} = 0\), find the value of \(\dfrac{x}{y}\), where \(y \ne 0\).
Login to check if your answer is correct.
Question 10
The last term of the sequence: 7, 11, 15, ... is 115. Find the number of terms in the sequence.
Login to check if your answer is correct.
Question 11
Find the mean deviation of 2, 5, 7, 9 and 15.
Login to check if your answer is correct.
Question 12
The locus, L is such that \(|PM| = |PN|\). Which of the following best describes L?
Login to check if your answer is correct.
Question 13
A train is moving at 60 miles per hour. If it passes a sign post in 15 seconds, find, in yards, the length of the train. [Take 1 mile = 1760 yards]
Login to check if your answer is correct.
Question 14
Kwaku is 2 years older than Atanga and 6 years younger than Esi. The sum of their ages is 70. If they decide to share USD 153.00 in the ratio of their ages, how much will the eldest person receive?
Login to check if your answer is correct.
Question 15
Solve: \(\dfrac{\log_{3}(2x - 1)}{\log_{3}243} = \dfrac{2}{5}\).
Login to check if your answer is correct.
Question 16
The sum of the ages of Esi and Amina is 24 years and the difference in their ages is 6 years. If Amina is older than Esi, find Esi's age.
Login to check if your answer is correct.
Question 17
Solve: \(4x + 1 \equiv 3(\text{mod }11)\).
Login to check if your answer is correct.
Question 18
Diagram will be provided In the diagram, \(|PQ| = 6.7\) cm, \(|QR| = 5.5\) cm and \(|RT| = 3.3\) cm. Find the area.
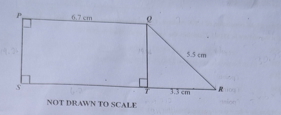

Login to check if your answer is correct.
Question 19
Diagram will be provided In the diagram, \(\triangle OMN\) is similar to \(\triangle OPQ\). Find \(|MQ|\).
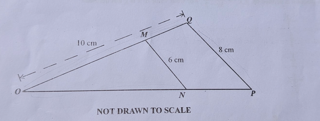

Login to check if your answer is correct.
Question 20
A scientific sensor records air pollution levels in base 3. If the highest recorded pollution level for a week was \(2120_3\), what is the decimal equivalent?
Login to check if your answer is correct.
Question 21
Factorize: \(5p^2 + 4pq - 15pr - 12qr\).
Login to check if your answer is correct.
Question 22
A school has a total population of 1,800 students. Out of this number \(\frac{4}{9}\) are in SHS 1, \(\frac{13}{36}\) are in SHS 2 and the rest are in SHS 3. Calculate the number of students in SHS 3.
Login to check if your answer is correct.
Question 23
The straight line \(3y + bx - 6 = 0\) passes through (3, 4). Find the value of \(b\).
Login to check if your answer is correct.
Question 24
A function is defined by \(g:x \rightarrow \dfrac{2x - 1}{3x - 2}\). For what value of x is g not defined?
Login to check if your answer is correct.
Question 25
Diagram will be provided In the diagram \(\angle QPR = 90^\circ\). If \(q^2 = 25 - r^2\), find the value of \(p\).
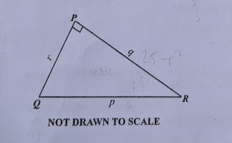

Login to check if your answer is correct.
Question 26
Diagram will be provided In the diagram \(PQRST\) is a trapezium. \(|ST| = 3\) cm, \(|RS| = y\) cm and \(|PS| = 4\) cm. For what values of \(y\) will the area of the trapezium \(PQRST\) be less than or equal to \(10\text{ cm}^2\)?
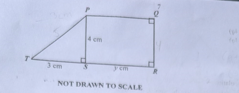

Login to check if your answer is correct.
Question 27
A town \(P\) is due south of town \(Q\) and town \(R\) is on a bearing of \(125^\circ\) from \(Q\). If town \(R\) is 20 km due east of \(P\), find \(|PQ|\).
Login to check if your answer is correct.
Question 28
Diagram will be provided The diagram shows a sector of a circle of radius 42 cm. If the sector is folded to form a right circular cone, find the surface area of the cone. [Take \(\pi = \frac{22}{7}\) ]
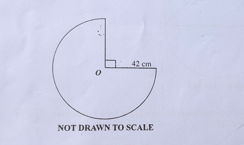

Login to check if your answer is correct.
Question 29
Diagram will be provided In the diagram, P, Q, R and S are points on the circle centre O and \(\angle PQR = 104^\circ\). Find the angle marked y.
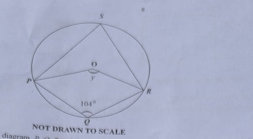

Login to check if your answer is correct.
Question 30
Diagram will be provided In the diagram \(\overline{TX}\) and \(\overline{TY}\) are tangents to the circle \(XYZ\) at \(X\) and \(Y\) respectively, \(\overline{TX} \parallel \overline{YZ}\) and \(\angle XTY = 100^\circ\). Find \(\angle ZXY\).
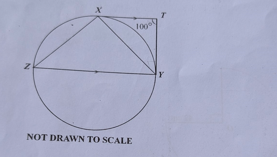

Login to check if your answer is correct.
Question 31
The radius of a circle is 4 times the radius of another circle. What is the relationship between their areas?
Login to check if your answer is correct.
Question 32
Diagram will be provided In the diagram, \(\angle QMP = 40^\circ\) and \(\angle RPM = 30^\circ\). Find the value of x.
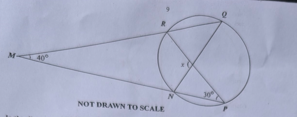

Login to check if your answer is correct.
Question 33
Some of the interior angles of a pentagon are 111°, 131° and 79°. The remaining angles are x and y in the ratio 2 : 3 respectively. Find, correct to the nearest whole number, the value of x.
Login to check if your answer is correct.
Question 34
Diagram will be provided In the diagram, P, Q, R and S are points on the circle centre O. \(\overline{QS}\) is a diameter and \(\angle ORQ = 41^\circ\). Find \(\angle QSR\).
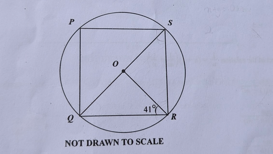

Login to check if your answer is correct.
Question 35
Diagram will be provided In the diagram, O is the centre of the circle and \(\angle OXZ = 19^\circ\). Find \(\angle XYZ\).
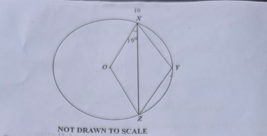

Login to check if your answer is correct.
Question 36
A car consumes 36 gallons of fuel over a distance of 2,268 km. Find, in km per litre, the fuel consumption. [Take 1 gallon = 4.5 litres]
Login to check if your answer is correct.
Question 37
Make \(w\) the subject of the relation \(\dfrac{1}{w} = (h - 1)\left(\dfrac{1}{m} - \dfrac{1}{n}\right)\).
Login to check if your answer is correct.
Question 38
The inverse of the sum of −3 and twice a certain number is \(\dfrac{1}{5}\). Find the number.
Login to check if your answer is correct.
Question 39
Diagram will be provided In the diagram, \(O\) is the centre of the circle, \(\angle KLM = x\) and \(|OM| = |ML| = |LK| = |KO|\). Find \(\angle OKL\).
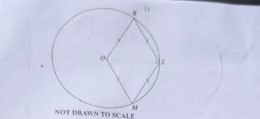

Login to check if your answer is correct.
Question 40
Diagram will be provided The diagram shows a field \(MNPQRST\), where \(MTS\) is a semicircle. Find the area of the field. [Take \(\pi = \dfrac{22}{7}\) ]
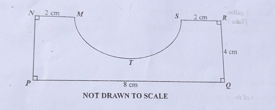

Login to check if your answer is correct.
Question 41
A box contains 12 red, 8 yellow and 10 green pebbles, all of the same size. If two pebbles are selected at random one after the other, with replacement, find the probability that the first is green and the second is not a red pebble.
Login to check if your answer is correct.
Question 42
Find the coefficient of \(x^2\) in the expansion of \((4x + 5)(3 - 2x)\).
Login to check if your answer is correct.
Question 43
Gifty is 19 years younger than her mother. In three years time the sum of their ages will be 67 years. Find the sum of their ages now.
Login to check if your answer is correct.
Question 44
A fair dice is thrown once. What is the probability of obtaining a 3 or 5?
Login to check if your answer is correct.
Question 45
The mean of \(a, b, c, d\) and \(e\) is 15. Calculate the mean of \((a + 1)\), \((b + 3)\), \((c + 5)\), \((d + 7)\) and \((e + 9)\).
Login to check if your answer is correct.
Question 46
If \(V = \pi r^2h\) and \(S = 2\pi rh\), express \(V\) in terms of \(r\) and \(S\).
Login to check if your answer is correct.
Question 47
A man cycles a distance of (3a) km at \(V\) km/h and then walks a distance of \(a\) km at \((V - 7)\) km/h. Find the total number of hours he spent travelling.
Login to check if your answer is correct.
Question 48
Peter is in the East of Tom and Tom is in the North of John. If Mike is in the South of John, in which direction of Peter is Mike?
Login to check if your answer is correct.
Question 49
Simplify: \(\dfrac{25p^{2}-q^{2}}{5p^{2}+6pq+q^{2}}\).
Login to check if your answer is correct.
Question 50
Correct. 5.40514 to three significant figures.
Login to check if your answer is correct.