Question 1
The sum of the interior angles of a polygon is 1260°. Find the number of sides.
Login to check if your answer is correct.
Question 2
A building is 12 m high. A football on the ground floor is 30 m away from the foot of the building. Find, correct to the nearest degree, the angle of depression of the ball from the top of the building.
Login to check if your answer is correct.
Question 3
A number is chosen at random from the set {13, 14, ...., 30}. What is the probability that it is a prime number?
Login to check if your answer is correct.
Question 4
Regina is 34 years old and her daughter is 5 years. In n years, Regina will be twice as old as her daughter. Find the value of n.
Login to check if your answer is correct.
Question 5
If P(−7, 8) is reflected in the line x − 2 = 0, find the coordinates of the image of P.
Login to check if your answer is correct.
Question 6
If the variable P is inversely proportional to Q² and P = 2.25 when Q = 6, find P when Q = 3.
Login to check if your answer is correct.
Question 7
Make x the subject of the relation: y = √(p x/r − r² x)
Login to check if your answer is correct.
Question 8
Seven men complete a certain work schedule in 6 days. How long will it take two of the men to complete the same work schedule if they work at the same rate?
Login to check if your answer is correct.
Question 9
If cos y is negative and sin y is negative, in which quadrant would y lie?
Login to check if your answer is correct.
Question 10
The volume of a cone is 264 cm³. If the base radius is 6 cm, find the height. [Take π = 22/7]
Login to check if your answer is correct.
Question 11
Find the value of x for which (2x − 1)/(x² + 2x + 1) is not defined.
Login to check if your answer is correct.
Question 12
The range of a sample of 10 numbers is 5 and the largest value is 50. What is the least value?
Login to check if your answer is correct.
Question 13
The mean of ten numbers is 16. When another number, k, is added, the mean becomes 18. Find the value of k.
Login to check if your answer is correct.
Question 14
The probability that John and James pass an examination are 3/4 and 3/5 respectively. Find the probability that both will fail.
Login to check if your answer is correct.
Question 15
The diagonals of a rhombus are 12 cm and 16 cm. Find the perimeter.
Login to check if your answer is correct.
Question 16
DIAGRAM WILL BE PROVIDED In the diagram PQR is a circle with centre O and ∠OQR = 42°. Find ∠QPR.
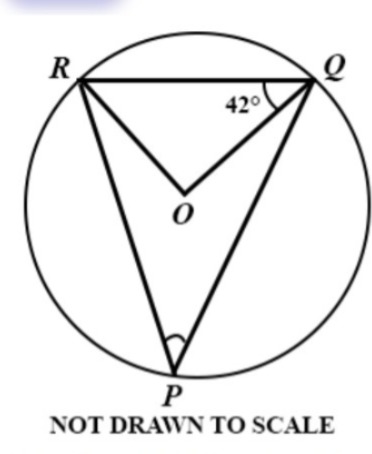

Login to check if your answer is correct.
Question 17
Solve: x(3x + 4) = 4.
Login to check if your answer is correct.
Question 18
If P = {−2, 0, 2, 4, 6} and Q = {−3, −1, 0, 2, 3, 5}, find the set P ∩ Q.
Login to check if your answer is correct.
Question 19
An office equipment depreciates at 15% per annum. If the cost is GH₵ 1,200.00 when new, find the value after three years.
Login to check if your answer is correct.
Question 20
Solve: (x − 2)/4 − (2x − 4)/3 = 5/6.
Login to check if your answer is correct.
Question 21
DIAGRAM WILL BE PROVIDED Calculate the value of t in the diagram.
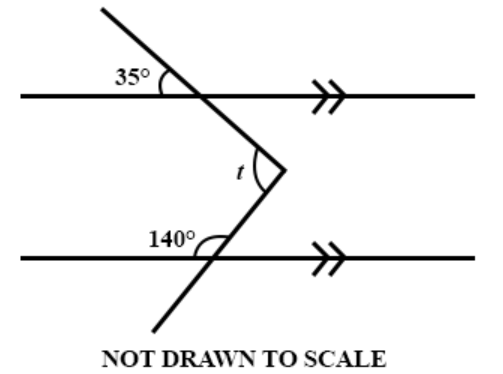

Login to check if your answer is correct.
Question 22
Given that 6 ⊗ 7 = y (modulo 8), find the value of y.
Login to check if your answer is correct.
Question 23
Express 0.0063075 correct to three significant figures.
Login to check if your answer is correct.
Question 24
Given statements p and q, the statement p ∨ q is false only if
Login to check if your answer is correct.
Question 25
What is the gradient of the equation of the line?


Login to check if your answer is correct.
Question 26
The table describes the relation y = mx + c where m and c are constants. Use the information to answer the question below Find the equation of the line described in the table.
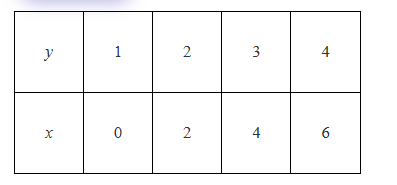

Login to check if your answer is correct.
Question 27
The second term of a Geometric Progression (G.P) is 9. If the fourth term is 81, find the common ratio.
Login to check if your answer is correct.
Question 28
DIAGRAM WILL BE PROVIDED In the diagram, ∆PQR is similar to ∆PWY. WY ∥ QR, QR = 15 cm, WY = 6 cm and WP = 4 cm. Find |WQ|.
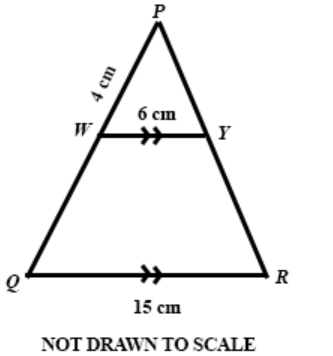

Login to check if your answer is correct.
Question 29
A cylindrical container closed at both ends has a radius of 3 cm and height of 4 cm. What is the total surface area of the container? [Take π = 22/7]
Login to check if your answer is correct.
Question 30
The diameter of a bicycle wheel is 21 cm. If the wheel makes 8 complete revolutions, what will be the total distance covered by the wheel? [Take π = 22/7]
Login to check if your answer is correct.
Question 31
DIAGRAM WILL BE PROVIDED Find the value of x in the diagram.
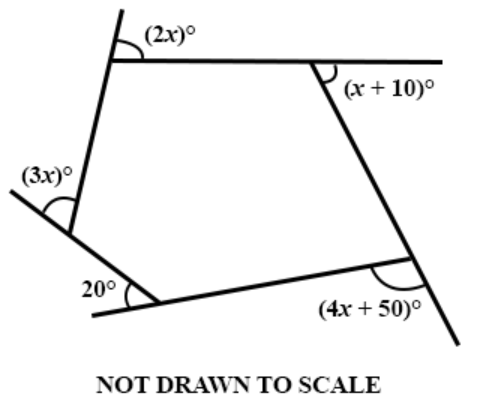

Login to check if your answer is correct.
Question 32
The interior angles of a triangle are (y + 10)°, (2y − 40)° and (3y − 90)°. Which of the following accurately describes the triangle?
Login to check if your answer is correct.
Question 33
Given that sin A = 3/5, 0° ≤ A ≤ 90°, find the value of (tan A − cos A).
Login to check if your answer is correct.
Question 34
Simplify: 3 log x + log y − 2 log z.
Login to check if your answer is correct.
Question 35
Simplify: a^(−1/4) × a^(1/2) ÷ a^(−1/2).
Login to check if your answer is correct.
Question 36
The area of a square parcel of land is 256 m². A rectangular field of length 20 m has the same perimeter as the parcel of land. Find the area of the field.
Login to check if your answer is correct.
Question 37
Mr. Abban invested USD 1,200.00 for 3 years at 5% per annum compound interest. Find the interest earned at the end of three years.
Login to check if your answer is correct.
Question 38
DIAGRAM WILL BE PROVIDED In the diagram PR is tangent to the circle at Q. The centre of the circle is O and ∠QOS = 108°. Use the information to answer the question below Find ∠OSQ.
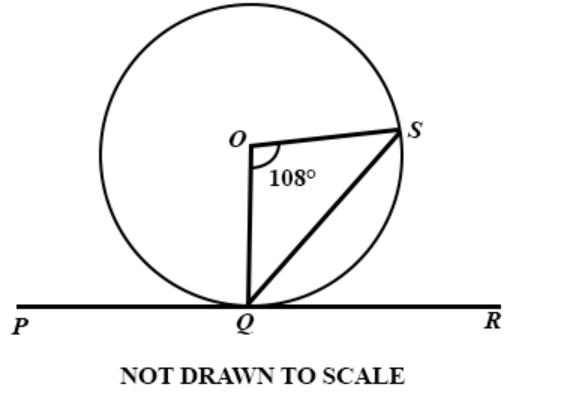

Login to check if your answer is correct.
Question 39
DIAGRAM WILL BE PROVIDED In the diagram PR is tangent to the circle at Q. The centre of the circle is O and ∠QOS = 108°. Use the information to answer the question below Find ∠SQR.
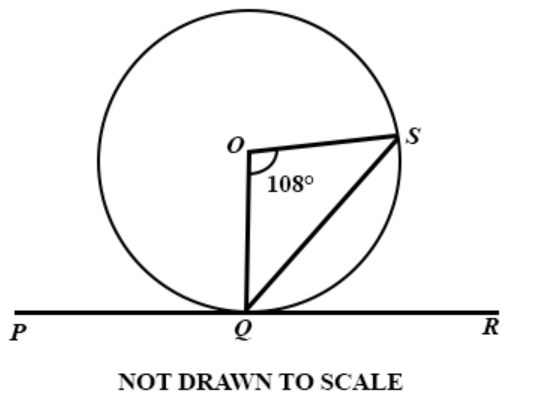

Login to check if your answer is correct.
Question 40
Find the value of x that satisfies the equation: 2/3 (x + 5) = 1 − (x − 7)/2.
Login to check if your answer is correct.
Question 41
A closed cuboid has length 12 cm, width 7 cm and height 5 cm. Calculate the total surface area.
Login to check if your answer is correct.
Question 42
Mr. Amuzu sold his car through an agent who charged 9% commission on the selling price. If Amuzu received GH₵ 236,600.00 after the sale, find the selling price of the car.
Login to check if your answer is correct.
Question 43
DIAGRAM WILL BE PROVIDED The diagram shows a triangle MNP inscribed in a circle. MQ is a tangent to the circle at M. Find ∠MPN.
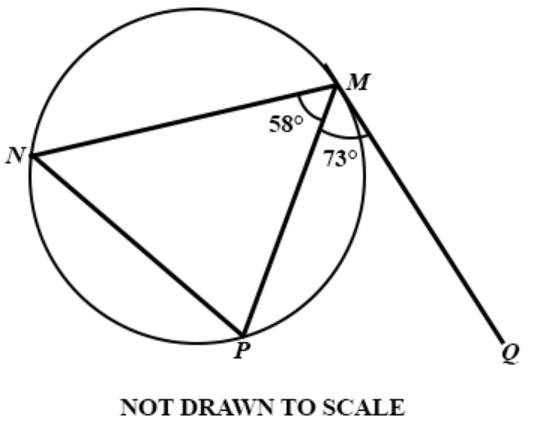

Login to check if your answer is correct.
Question 44
In an examination taken by 120 students, 90 passed Mathematics, 40 passed Science and 5 failed both subjects. Use the information to answer the question below How many students passed Science only
Login to check if your answer is correct.
Question 45
In an examination taken by 120 students, 90 passed Mathematics, 40 passed Science and 5 failed both subjects. Use the information to answer the question below Find the probability that a student selected at random passed only one subject.
Login to check if your answer is correct.
Question 46
DIAGRAM WILL BE PROVIDED In the diagram, PR is a diameter of the circle PQS with centre O. Find ∠PQS.
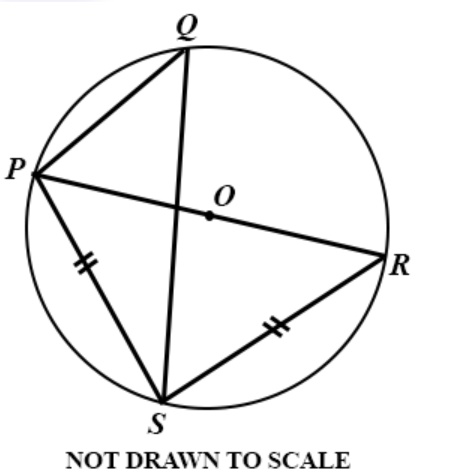

Login to check if your answer is correct.
Question 47
If P(−7, 8) is reflected in the line x − 2 = 0, find the coordinates of the image of P.
Login to check if your answer is correct.
Question 48
Find the product of 124(seven) and 23(seven).
Login to check if your answer is correct.
Question 49
Given that m = 5, n = 3 and r = 2, evaluate (m² − n²) + r² / (m² + (n² − r²)).
Login to check if your answer is correct.
Question 50
Three boys of ages 2, 4 and 10 shared 32 oranges in the ratio of their ages. What was the least share?
Login to check if your answer is correct.