Question 1
A point on the ground is 5 m away from the foot of a vertical wall 12 m high. Calculate, correct to the nearest degree, the angle of depression of the point from the top of the wall.
Login to check if your answer is correct.
Question 2
The gradient of the line passing through the points (3, 6) and (x, 4) is (-\frac{2}{5}). Find the value of x.
Login to check if your answer is correct.
Question 3
A woman pours 85 litres of kerosene into a cylindrical container with radius 7 cm. Calculate, correct to the nearest cm, the depth of the kerosene in the container. [\text{Take } \pi = \frac{22}{7}]
Login to check if your answer is correct.
Question 4
Given that (x^2 - 11x + m) is a perfect square, find the value of m.
Login to check if your answer is correct.
Question 5
The sides of a scalene triangle are 4 cm, 9 cm and 11 cm. Calculate, correct to the nearest whole number, the area of the triangle.
Login to check if your answer is correct.
Question 6
In a hall, there are 175 persons. 12% are children, 56 are men and the rest are women. If one person is selected at random from the hall, find the probability that a woman is selected.
Login to check if your answer is correct.
Question 7
A student measured the length of a classroom and obtained 3.99 m which is less than the actual length. If the percentage error was 5%, what was the actual length?
Login to check if your answer is correct.
Question 8
A car covers the first 80 km of a journey in 2 hours and completes the journey by travelling further 2.5 hours at 50 km/h. What is the average speed of the entire journey?
Login to check if your answer is correct.
Question 9
If (\log x = 2 - 3\log 2), find the value of x.
Login to check if your answer is correct.
Question 10
The graph of (y = x^2 - 5x + k) passes through the point (3, 1). Find the value of k.
Login to check if your answer is correct.
Question 11
Diagram will be provided Find the value of x in the diagram.
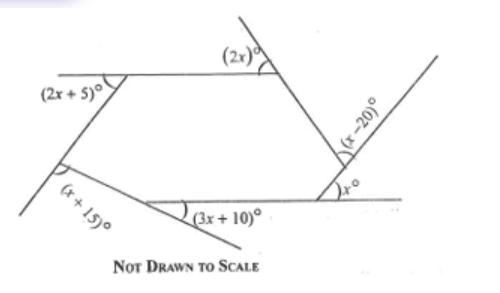

Login to check if your answer is correct.
Question 12
Diagram will be provided In the diagram, (p + q = 250^\circ). Find the angle marked s.
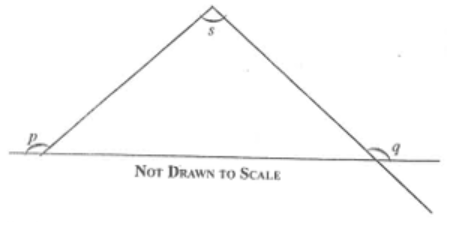

Login to check if your answer is correct.
Question 13
If (x : y : z = 2 : 3 : 4), evaluate (\dfrac{9x + 3y}{6z - 2y}).
Login to check if your answer is correct.
Question 14
Find the mean of ((x + y)), ((2x + 3y)), ((2x - 2y)) and ((3x - 2y)).
Login to check if your answer is correct.
Question 15
A box contains 2 red, 6 white and 5 black balls, all of the same size. If a ball is selected at random, what is the probability that it is black?
Login to check if your answer is correct.
Question 16
Diagram will be provided In the diagram, MNPQ is a circle, centre O. (\angle MQN = 43^\circ) and (\angle QNP = 57^\circ). Find the value of y.
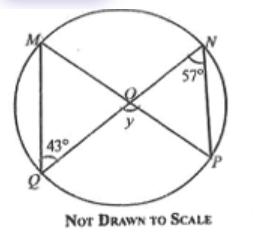

Login to check if your answer is correct.
Question 17
Diagram will be provided Describe the locus, l in the diagram.
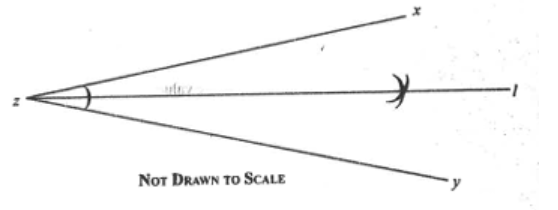

Login to check if your answer is correct.
Question 18
The base radius and slant height of a solid cone are 8 cm and 14 cm respectively. Calculate, correct to two decimal places, its volume. [\text{Take } \pi = \frac{22}{7}]
Login to check if your answer is correct.
Question 19
Abudu can do a piece of work in 6 days and Efah can do the same work in 3 days. What fraction of the work can both do together in a day?
Login to check if your answer is correct.
Question 20
If (P = {x: 1 \le x \le 6}) and (Q = {x: 2 < x < 9}) where (x \in R), find (P \cap Q).
Login to check if your answer is correct.
Question 21
Given that (p^2 + q^2 + r^2 = 50), (p = 5) and (\sqrt{q} = 2), find the positive value of r.
Login to check if your answer is correct.
Question 22
If (\frac{1}{2}) and -3 are the roots of (px^2 + qx + r = 0), find the values of p, q and r.
Login to check if your answer is correct.
Question 23
A cylindrical container closed at both ends has radius 5 cm and height 10 cm. Calculate to two decimal places, the total surface area. [\text{Take } \pi = \frac{22}{7}]
Login to check if your answer is correct.
Question 24
Badu is four times as old as Juliet. In 10 years Badu will be twice as old as Juliet. Find Juliet's age.
Login to check if your answer is correct.
Question 25
When the point (4, 5) is rotated through an angle in the anticlockwise direction about the origin, its image is (-5, 4). What is the angle of rotation?
Login to check if your answer is correct.
Question 26
Diagram will be provided Find the value of x in the diagram.
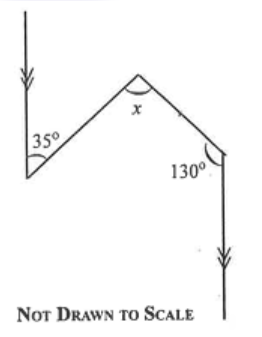

Login to check if your answer is correct.
Question 27
A woman bought a washing machine for USD 18,000.00. If the exchange rate is USD 0.045 to ₦1.00, find in ₦, the cost of the machine.
Login to check if your answer is correct.
Question 28
Determine the least value of x such that (7 + x \equiv 3 \pmod{8}).
Login to check if your answer is correct.
Question 29
If (\dfrac{4m + 3n}{4m - 3n} = \frac{5}{2}), find the ratio of m : n.
Login to check if your answer is correct.
Question 30
Yakubu received (12\frac{1}{2}%) of the sales made in a certain mouth. If the amount he received was USD 35,000.00, what was the total sales made?
Login to check if your answer is correct.
Question 31
The angle of elevation of the top of a vertical pole from a point, P on a level ground is 60°. The distance from P to the foot of the pole is 55 m. Find the height of the pole.
Login to check if your answer is correct.
Question 32
The ratio of girls to boys in a certain committee is 5 : 2. If there are 35 members in the committee, how many more boys must be added to the committee to have the ratio of girls to boys as 5 : 4?
Login to check if your answer is correct.
Question 33
Find the values of x for which (\dfrac{x + 1}{3x^2 - 12}) is not defined.
Login to check if your answer is correct.
Question 34
Given that (\tan x = \frac{12}{5}), find the value of ((\sin x \cos x))
Login to check if your answer is correct.
Question 35
Consider these two statements: P: N is an odd number Q: N is a prime number greater than 2. Express "If N is not an odd number then N is not a prime number greater than 2" in symbolic form.
Login to check if your answer is correct.
Question 36
A sector which subtends an angle 150° is cut from a circular plate of radius 14 cm. Find, correct to one decimal place, the perimeter of the remaining plate. [\text{Take } \pi = \frac{22}{7}]
Login to check if your answer is correct.
Question 37
One side of a gutter is 15 cm lower than the other side. A plank of wood, which is laid across the gutter to form a bridge, slopes at an angle of 35° to the horizontal. How wide is the gutter?
Login to check if your answer is correct.
Question 38
Diagram will be provided In the diagram, MOP is the diameter of the circle MNP centre O. (\angle NMP = (2x)^\circ) and (\angle EPM = (5x + 18)^\circ). Find the value of x.
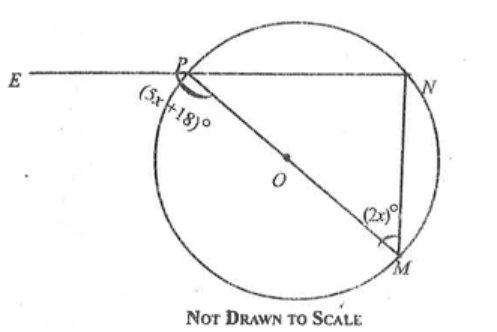

Login to check if your answer is correct.
Question 39
The height of a square base pyramid is thrice the length of a side of its base. If the base area is 324 cm², find the volume of the pyramid.
Login to check if your answer is correct.
Question 40
If (4^x = \frac{1}{1024}), find the value of x
Login to check if your answer is correct.
Question 41
"Diagram will be provided" In the diagram, O is the centre of the circle WXY. (|WX| = |XZ|) and (\angle ZXY = 26^\circ). Find (\angle XYZ).
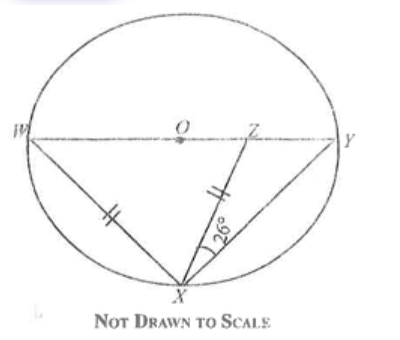

Login to check if your answer is correct.
Question 42
Evaluate (141_6 + 233_6 - 102_6)
Login to check if your answer is correct.
Question 43
In the first year, Mr. Kwakye's annual salary was USD 1,560.00. His salary was increased each year by a constant value, y until it was USD 13,980.00 in the 13th year. Calculate the value of y.
Login to check if your answer is correct.
Question 44
Given that (\frac{16}{9}, x, 1, y) is a Geometric Progression (G.P), find the value of xy.
Login to check if your answer is correct.
Question 45
A chord of a circle, 12 cm long subtends an angle of 150° at the centre of the circle. Find the radius of the circle.
Login to check if your answer is correct.
Question 46
The lines (3x + 2y = 4) and (y = 2x - 5) intersect at a point P(x, y). Find the coordinates of P.
Login to check if your answer is correct.
Question 47
Make u the subject of the relation (\dfrac{t}{s+u} = \dfrac{s}{t-u}).
Login to check if your answer is correct.
Question 48
"Table will be provided"The table shows the number of subjects registered by a class of students for an examination. Use the information to answer the question below Calculate the mean of the distribution.


Login to check if your answer is correct.
Question 49
"Table will be provided" The table shows the number of subjects registered by a class of students for an examination. Use the information to answer the question below Find the median.


Login to check if your answer is correct.
Question 50
A rectangular tank of sides 4 m by 8 m by 11 m has the same volume as a cylindrical tank of height 7 m. Calculate the base radius of the cylindrical tank. [\text{Take } \pi = \frac{22}{7}]
Login to check if your answer is correct.