Question 1
Find the number of even integers between 11 and 97.
Login to check if your answer is correct.
Question 2
Find the values of \(x\) for which \(\dfrac{1}{2x^{2}-13x+15}\) is not defined.
Login to check if your answer is correct.
Question 3
**DIAGRAM WILL BE PROVIDED.** In the diagram, \(P,Q,R,S\) are points on the circle. If \(\angle PQS = 32^\circ\) and \(\angle PRQ = 61^\circ\), find \(\angle QPS\).
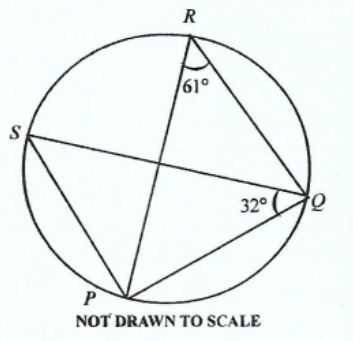

Login to check if your answer is correct.
Question 4
The bearing of a point \(P\) from a point \(Q\) is \(065^\circ\). What is the bearing of \(Q\) from \(P\)?
Login to check if your answer is correct.
Question 5
The arc of a circle \(50\ \text{cm}\) long subtends an angle \(75^\circ\) at the centre of the circle. Find, correct to three significant figures, the radius of the circle. \([Take\ \pi=\frac{22}{7}]\)
Login to check if your answer is correct.
Question 6
Find the truth set of \((3 + x)(1 - x) > 9 - x^{2}\).
Login to check if your answer is correct.
Question 7
A bag contains 32 blue, 28 black and 20 red identical balls of same size. If a ball is picked at random, what is the probability that it is not red?
Login to check if your answer is correct.
Question 8
Simplify: \(\frac{1}{2}(x-1)-\frac{1}{3}\left(\frac{1}{2}x-1\right)\).
Login to check if your answer is correct.
Question 9
A woman buys 3 exercise books at GH₵ 0.4 each and 9 exercise books at GH₵ 0.2 each. What is the average cost of an exercise book?
Login to check if your answer is correct.
Question 10
Given that \(4x + 6y = 5\) and \(2x + 4y = 3\), find the value of \((x + 2y)\).
Login to check if your answer is correct.
Question 11
Simplify \(\dfrac{9-x^{2}}{3x-x^{2}}\), where \(x \ne 3\).
Login to check if your answer is correct.
Question 12
Given that \(P \propto v^{2}x\) and \(x \propto vt\), express \(P\) in terms of \(v\) and \(t\).
Login to check if your answer is correct.
Question 13
Express, correct to two significant figures \(\left(\frac{9}{28}-\frac{2}{7}\right)\).
Login to check if your answer is correct.
Question 14
**DIAGRAM WILL BE PROVIDED.** Find the value of \(y\) in the diagram.
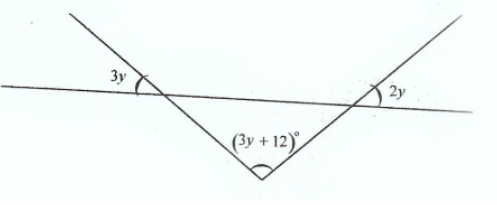

Login to check if your answer is correct.
Question 15
If \((23)_{x} = (1111)_{two}\), find the value of \(x\).
Login to check if your answer is correct.
Question 16
Dina and Rose were given GH₵ 875.08 to be shared in the ratio 3:2 respectively. If Rose shared her part of the money between Efua and Ama in the ratio 1:2 respectively, how much was Ama's share?
Login to check if your answer is correct.
Question 17
If \(9^{\,y+1} = \left(\frac{1}{27}\right)^{\,y-2}\), find \(y\).
Login to check if your answer is correct.
Question 18
A market woman demands GH₵ 15.00 for a tin of local rice. After some bargaining with a customer, she sells 5 tins for GH₵ 66.00. By what percentage did she reduce her original price?
Login to check if your answer is correct.
Question 19
The graph of \(y = x^{2} + 4x - 6\) is drawn and a linear graph is drawn on the axes such that the intersection of the two graphs gives the solution to the equation \(x^{2} + 4x - 7 = 0\). Find the equation for the linear graph.
Login to check if your answer is correct.
Question 20
The interior angle of a regular polygon is twice the exterior angle. How many sides has the polygon?
Login to check if your answer is correct.
Question 21
Metuh is nine times as old as his cousin, Fafa. In six years time, he will be five times as old as Fafa. Find Fafa's present age.
Login to check if your answer is correct.
Question 22
If \(A=\frac{1}{2}b(a + b)\), make \(a\) the subject of the relation.
Login to check if your answer is correct.
Question 23
Evaluate \(\dfrac{53,000,000 \times 0.002}{0.0004}\).
Login to check if your answer is correct.
Question 24
If \(\frac{x + y}{5} = \frac{x - y}{3}\), find \(x:y\).
Login to check if your answer is correct.
Question 25
Find the equation of the line passing through \(P(4,1)\) and parallel to \(2x + 5y = -10\).
Login to check if your answer is correct.
Question 26
The exterior angles of a quadrilateral are \(61^\circ,76^\circ,(x+10)^\circ\) and \((2x+45)^\circ\). Find the value of \(x\).
Login to check if your answer is correct.
Question 27
If \(17 \equiv 3 \pmod{x}\), find the least value of \(x\).
Login to check if your answer is correct.
Question 28
The shadow of a vertical pole is 50 cm. If the height of the pole is 2 m, find, correct to the nearest degree, the angle of elevation of the sun from the ground level.
Login to check if your answer is correct.
Question 29
Consider the following statements: M: Helena studies hard; N: Helena passes her examination. If \(M \Rightarrow N\)
Login to check if your answer is correct.
Question 30
The area of a sector of a circle is \(40\ \text{cm}^{2}\). If the sector subtends an angle of \(140^\circ\) at the centre, find the area of the circle.
Login to check if your answer is correct.
Question 31
Given that \(6\log(x + 4) = \log 64\), find the value of \(x\).
Login to check if your answer is correct.
Question 32
A die is rolled once. Find the probability of obtaining a number less than 3.
Login to check if your answer is correct.
Question 33
**DIAGRAM WILL BE PROVIDED.** If the area of the trapezium \(MNOP\) is \(300\ \text{cm}^{2}\), find the value of \(x\).
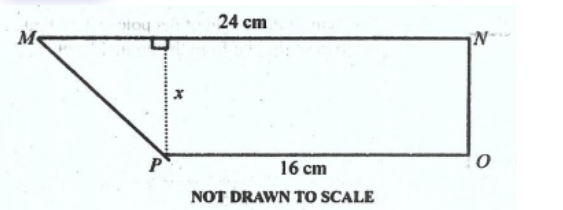

Login to check if your answer is correct.
Question 34
Find the 11th term of \(\frac{1}{4},\frac{5}{8},1,\frac{13}{8}, \ldots\).
Login to check if your answer is correct.
Question 35
In a class of 30 students, 18 takes Mathematics, 5 take both Mathematics and Biology and 8 take neither Mathematics nor Biology. Find the number of students that take Biology.
Login to check if your answer is correct.
Question 36
**DIAGRAM WILL BE PROVIDED.** In the diagram, \(MN // PQ\). Find the value of \((x + y)\).
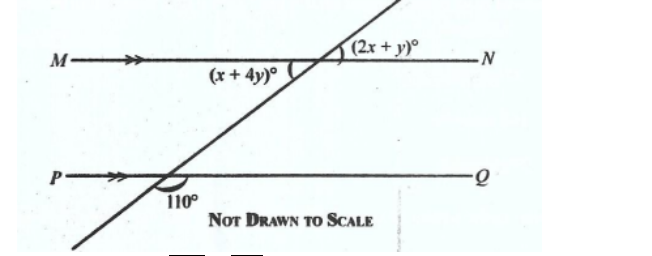

Login to check if your answer is correct.
Question 37
Simplify \(\dfrac{\sqrt{3}+\sqrt{48}}{\sqrt{6}}\).
Login to check if your answer is correct.
Question 38
The length of a rectangular lawn is 3 cm longer than the width. If the perimeter is 42 cm, find the width.
Login to check if your answer is correct.
Question 39
Given that \(p=x-\frac{1}{x}\) and \(q=x^{2}+\frac{1}{x^{2}}\), express \(q\) in terms of \(p\).
Login to check if your answer is correct.
Question 40
A car moves at an average speed of 30 kmh\(^{-1}\). How long does it take to cover 200 metres?
Login to check if your answer is correct.
Question 41
If \(y\) varies as the square of \(x\), \(y = 3\) when \(x = \sqrt{2}\), find the value of \(y\) when \(x = 2\).
Login to check if your answer is correct.
Question 42
**DIAGRAM WILL BE PROVIDED.** In the diagram, \(O\) is the centre of the circle \(PQR\), \(|PS| = |PQ|\) and \(\angle RQS = 23^\circ\). Find the value of \(x\).
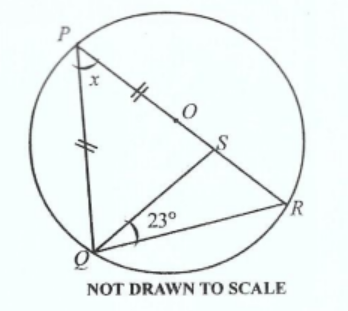

Login to check if your answer is correct.
Question 43
The mass of some market women in kg are: 83, 47, 62, 49, 55, 72, 58 and 62. Find the range.
Login to check if your answer is correct.
Question 44
The mass of some market women in kg are: 83, 47, 62, 49, 55, 72, 58 and 62. Find the mean.
Login to check if your answer is correct.
Question 45
Evaluate \(\tan 30^\circ - 2\sin 60^\circ\).
Login to check if your answer is correct.
Question 46
Simplify: \(8\frac{1}{6}-\left(11\frac{2}{3}\div 2\frac{2}{3}\right)\).
Login to check if your answer is correct.
Question 47
The probabilities of three independent events \(X, Y\) and \(Z\) occurring are \(\frac{1}{2}, \frac{2}{3}\) and \(\frac{1}{4}\) respectively. What is the probability that only events \(X\) and \(Z\) are occurring?
Login to check if your answer is correct.
Question 48
One side of a rectangle is 8 cm and the diagonal is 10 cm. Calculate the area of the rectangle.
Login to check if your answer is correct.
Question 49
**DIAGRAM WILL BE PROVIDED.** In the diagram, \(EFGH\) are points on a circle centre \(P\). If \(\angle EFG = 142^\circ\) and \(\angle FGP = 63^\circ\), find \(\angle FEP\).
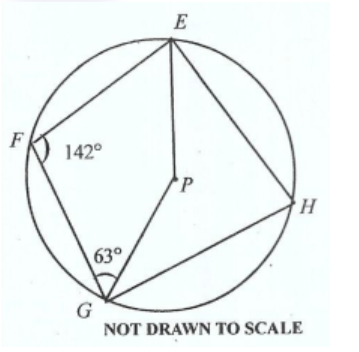

Login to check if your answer is correct.
Question 50
**DIAGRAM WILL BE PROVIDED.** In the diagram \(PQ\) is the diameter of circle \(PQR\) with centre \(O\) and \(RS\) meets \(PQ\) at \(S\). If \(\angle RQP = 64^\circ\) and \(\angle RSQ = 36^\circ\), find \(\angle PRS\).
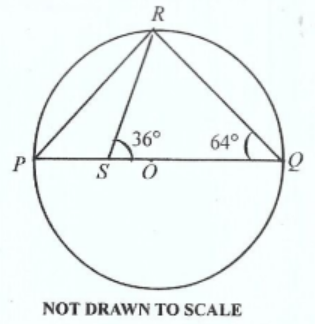

Login to check if your answer is correct.