Question 1
Correct 0.00798516 to three significant figures.
Login to check if your answer is correct.
Question 2
Simplify: \((11)_2\)^2
Login to check if your answer is correct.
Question 3
Solve: \(2^{\sqrt{2x + 1}} = 32\)
Login to check if your answer is correct.
Question 4
If \(\log_{10} 2 = m\) and \(\log_{10} 3 = n\), find \(\log_{10} 24\) in terms of m and n.
Login to check if your answer is correct.
Question 5
Find the 5th term of the sequence 2, 5, 10, 17....?
Login to check if your answer is correct.
Question 6
If \(P = \{-3 < x < 1\}\) and \(Q = \{-1 < x < 3\}\), where x is a real number, find \(P \cap Q\).
Login to check if your answer is correct.
Question 7
Factorize \(6pq - 3rs - 3ps + 6qr\).
Login to check if your answer is correct.
Question 8
What number should be subtracted from the sum of \(2\frac{1}{6}\) and \(2\frac{7}{12}\) to give \(3\frac{1}{4}\)?
Login to check if your answer is correct.
Question 9
Mensah is 5 years old and Joyce is thrice as old as Mensah. In how many years will Joyce be twice as old as Mensah?
Login to check if your answer is correct.
Question 10
If \(16 \times 2^{(x + 1)} = 4^{x} \times 8^{(1 − x)}\), find the value of x.
Login to check if your answer is correct.
Question 11
The circumference of a circular track is 9 km. A cyclist rides round it a number of times and stops after covering a distance of 302 km. How far is the cyclist from the starting point?
Login to check if your answer is correct.
Question 12
Simplify \(2\sqrt{7} - \frac{14}{\sqrt{7}} + \frac{7}{\sqrt{21}}\)
Login to check if your answer is correct.
Question 13
If \(4x + 2y = 16\) and \(6x - 2y = 4\), find the value of \((y - x)\).
Login to check if your answer is correct.
Question 14
Given that R is directly proportional to L and inversely proportional to P, R = 3 when L = 9 and P = 0.8, find R when L = 15 and P = 1.8.
Login to check if your answer is correct.
Question 15
**DIAGRAM WILL BE PROVIDED.** In the diagram, \(\angle ABC\) and \(\angle BCD\) are right angles, \(\angle BAD = t\) and \(\angle EDF = 70^\circ\). Find the value of t.
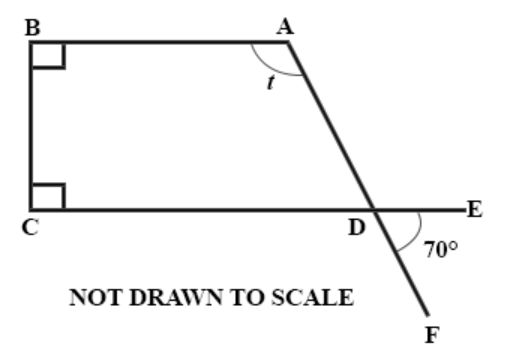

Login to check if your answer is correct.
Question 16
The sum of the interior angles of a regular polygon with k sides is (3k - 10) right angles. Find the size of the exterior angle.
Login to check if your answer is correct.
Question 17
Make U the subject of the relation: \(x = \frac{2U - 3}{3U + 2}\).
Login to check if your answer is correct.
Question 18
A trader paid import duty of 38 kobo in the naira on the cost of an engine. If a total of ₦ 22,800.00 was paid as import duty, calculate the cost of the engine.
Login to check if your answer is correct.
Question 19
The height of an equilateral triangle is \(10\sqrt{3}\) cm. Calculate its perimeter.
Login to check if your answer is correct.
Question 20
In a \(\triangle LMN\), \(|LM| = 6\) cm, \(\angle LMN = 90^\circ\), \(\angle LNM = x\) and \(\sin x = \frac{3}{5}\). Find the area of \(\triangle LMN\).
Login to check if your answer is correct.
Question 21
**DIAGRAM WILL BE PROVIDED.** Consider the statements: P: = All students offering Literature(L) also offer History(H); Q: = Students offering History(H) do not offer Geography(G). Which of the Venn diagram correctly illustrate the two statements?
Login to check if your answer is correct.
Question 22
Find The quadratic Equation whose roots are \(-2q\) And \(5q\).
Login to check if your answer is correct.
Question 23
If \(\tan \theta = \frac{3}{4}\), \(180^\circ < \theta < 270^\circ\), find the value of \(\cos \theta\).
Login to check if your answer is correct.
Question 24
If \(\frac{2}{(x - 3)} - \frac{3}{(x - 2)} = \frac{p}{(x - 3)(x - 2)}\), find p.
Login to check if your answer is correct.
Question 25
The diagonal of a rhombus are 12 cm and 5 cm. Calculate its perimeter.
Login to check if your answer is correct.
Question 26
**DIAGRAM WILL BE PROVIDED.** In the diagram, \(\triangle XYZ\) is produced to T. If \(|XY| = |ZY|\) and \(\angle XYT = 40^\circ\), find \(\angle XZT\).
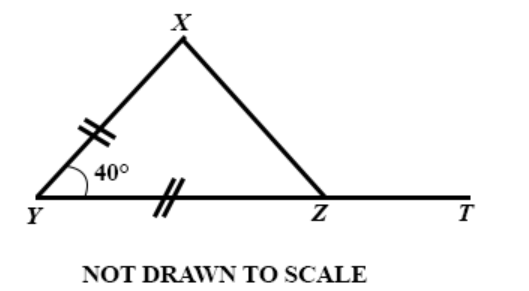

Login to check if your answer is correct.
Question 27
A solid brass cube is melted and recast as a solid cone of height h and base radius r. If the height of the cube is h, find r in terms of h.
Login to check if your answer is correct.
Question 28
Which of the following is not an exterior angle of a regular polygon?
Login to check if your answer is correct.
Question 29
From a point T, a man moves 12 km due West and then moves 12 km due South to another point Q. Calculate the bearing of T from Q.
Login to check if your answer is correct.
Question 30
**DIAGRAM WILL BE PROVIDED.** In the diagram, O is the centre of the circle PQRS, \(\angle PQR = 72^\circ\) and \(OR\parallel PS\). Find \(\angle OPS\).
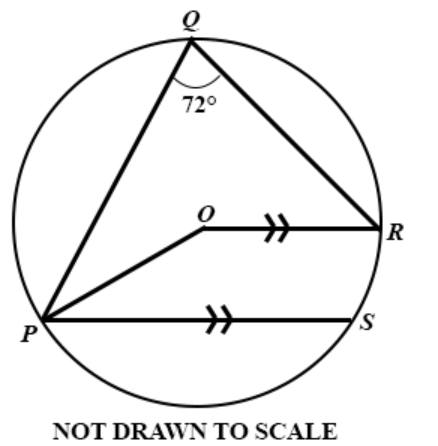

Login to check if your answer is correct.
Question 31
A trapezium of parallel sides 10 cm and 21 cm and height 8 cm is inscribed in a circle of radius 7 cm. Calculate the area of the region not covered by the trapezium. [Take \(\pi = \frac{22}{7}\)]
Login to check if your answer is correct.
Question 32
Find correct to two decimal places the mean of \(1\frac{1}{2},\;2\frac{2}{3},\;3\frac{3}{4},\;4\frac{4}{5}\) and \(5\frac{5}{6}\).
Login to check if your answer is correct.
Question 33
A cyclist moved at a speed of X km/h for 2 hours. He then increased his speed by 2 km/h for the next 3 hours. If the total distance covered is 36 km, calculate his initials speed.
Login to check if your answer is correct.
Question 34
**DIAGRAM WILL BE PROVIDED.** Find the value of \((x + y)\) in the diagram.
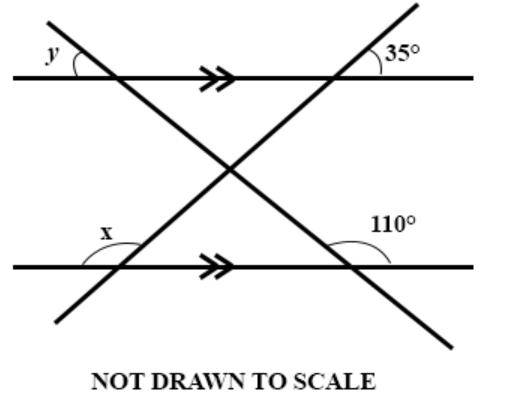

Login to check if your answer is correct.
Question 35
**DIAGRAM WILL BE PROVIDED.** In the diagram, MP is a tangent to the circle NQR, \(\angle PNQ = 64^\circ\) and \(|RQ| = |RN|\). Find the angle marked t.
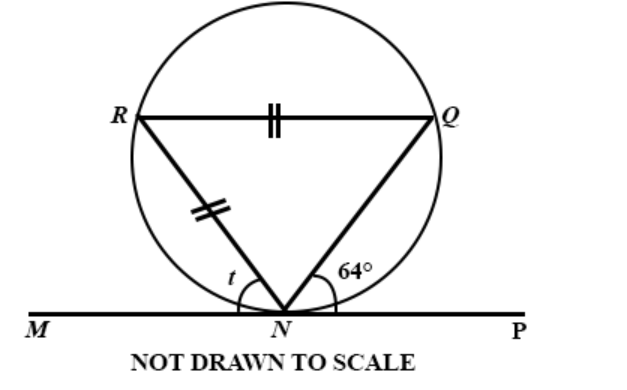

Login to check if your answer is correct.
Question 36
Find the first quartile of 7, 8, 7, 9, 11, 8, 7, 9, 6 and 8.
Login to check if your answer is correct.
Question 37
**DIAGRAM WILL BE PROVIDED.** In the diagram, PQRS is a circle. find the value of x.
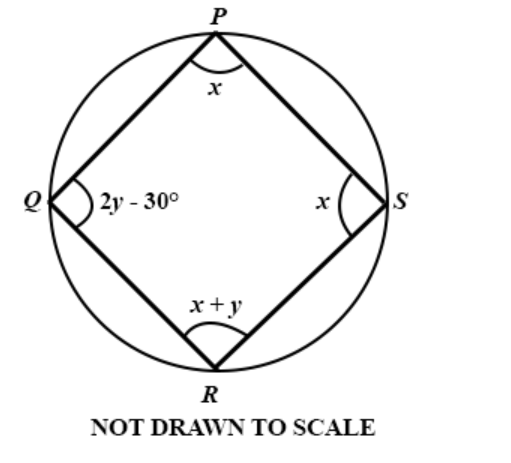

Login to check if your answer is correct.
Question 38
A cone has a base radius of 8 cm and height 11 cm. Calculate, correct to two decimal places, the curved surface area. [Take \(\pi = \frac{22}{7}\)]
Login to check if your answer is correct.
Question 39
Given that \(\sin x = \frac{3}{5}\), \(0^\circ \le x \le 90^\circ\), evaluate \((\tan x + 2\cos x)\).
Login to check if your answer is correct.
Question 40
**DIAGRAM WILL BE PROVIDED.** In the diagram \(EC\) is a diameter of circle ABCDE. If \(\angle ABC = 158^\circ\), find \(\angle ADE\).
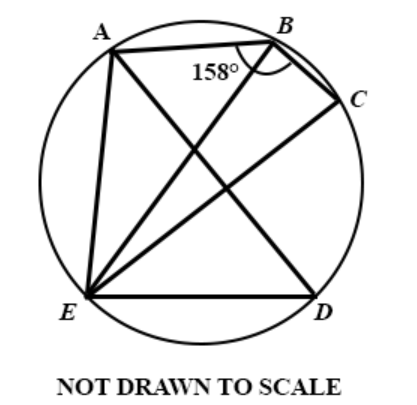

Login to check if your answer is correct.
Question 41
**TABLE WILL BE PROVIDED.** The table shows the heights of thirty-seven players of a basketball team. Calculate, correct to one decimal place, the mean height of the players.


Login to check if your answer is correct.
Question 42
XY is a line segment with the coordinates X(-8, -12) and Y(p, q). If the midpoint of XY is (-4, -2), find the coordinates of Y.
Login to check if your answer is correct.
Question 43
Five hundred tickets were sold for a concert. Tickets for adults and children were sold at USD 4.50 and USD 3.00, respectively. If the total receipts for the concerts was USD 1987.50, how many tickets for adults were sold?
Login to check if your answer is correct.
Question 44
The distance (d) between two villages is more than 18 km but not more than 23 km. Which of these inequalities represents the statements?
Login to check if your answer is correct.
Question 45
**DIAGRAM WILL BE PROVIDED.** The pie chart represents the distribution of fruits on display in a shop. If there are 60 apples on display, how many oranges are there?
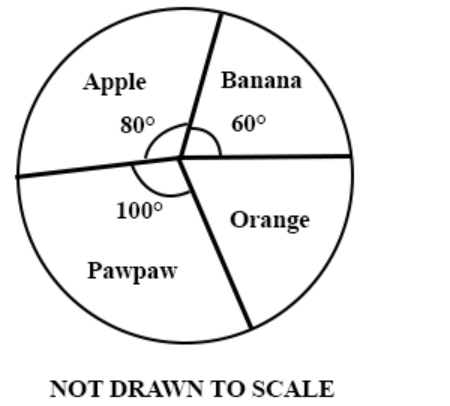

Login to check if your answer is correct.
Question 46
A box contains 40 identical balls of which 10 are red and 12 are blue. If a ball is selected at random from the box, what is the probability that it is neither red nor blue?
Login to check if your answer is correct.
Question 47
A fair die is tossed twice. What is the probability of getting a sum of at least 10?
Login to check if your answer is correct.
Question 48
A man will be (x + 10) years old in 8 years time. If 2 years ago he was 63 years, find the value of x
Login to check if your answer is correct.
Question 49
The equation of a line is given as 3x - 5y = 7. Find its gradient (slope).
Login to check if your answer is correct.
Question 50
For what value of x is \(4 - \frac{2x}{x + 1}\) undefined?
Login to check if your answer is correct.